Multi-dimensional Spatial Voting Simulations¶
John Huang, 25 May 2020
Executive Summary¶
This report documents simulation results for multi-dimensional spatial election models. In these simulations:
The number of candidates was varied from 3, 4, 5, 7, and 9.
Candidates were uniformly generated within 1.5 standard deviations of voter population preferences.
The number of preference dimensions was varied from 1 to 5.
All elections had 101 voters generated from a normal distribution.
All voters were assumed to grade candidates relative to their best and worst candidate.
Other details about the voting model and assessment methodology are presented in the previous report for 3-way elections.
Assessed systems include:
These new systems are compared to the traditional plurality voting system.
From these simulations we can draw the following conclusions:
For 1-dimensional models, Condorcet methods such as ranked pairs and smith-minimax have superior performance.
Increasing preference dimensions from 1 to 2 increases the prevalence of Condorcet Paradoxes from 0% to 5.15%.
Increasing preference dimensions reduces Condorcet method satisfaction.
Cardinal methods have excellent multi-dimensional performance. At 5 dimensions, score is the best performing system.
The best, well-rounded methods are hybrid methods such as STAR voting and Smith-Minimax for 1-dimensional, 2-dimensional and multi-dimensional performance.
1-Dimensional vs 2-Dimensional Models¶
Newly generated scenario categorization for 1 and 2 preference dimensions are shown below. The following observations can be made:
The transition to 2-dimensions increases the occurrence of Condorcet Paradoxes from 0% to 5.152%.
The transition to 2-dimensions also increases the occurrence of Condorcet failures, where the Condorcet winner is not coincident with the Utility winner (Scenarios C, CP, PU, and M) from 3.75% to 12.28%
The transition to 2-dimensions changes the most likely scenario from “CU” (49.824% to 34.526% of scenarios) to “CPU” (27.736% to 36.58% of scenarios).
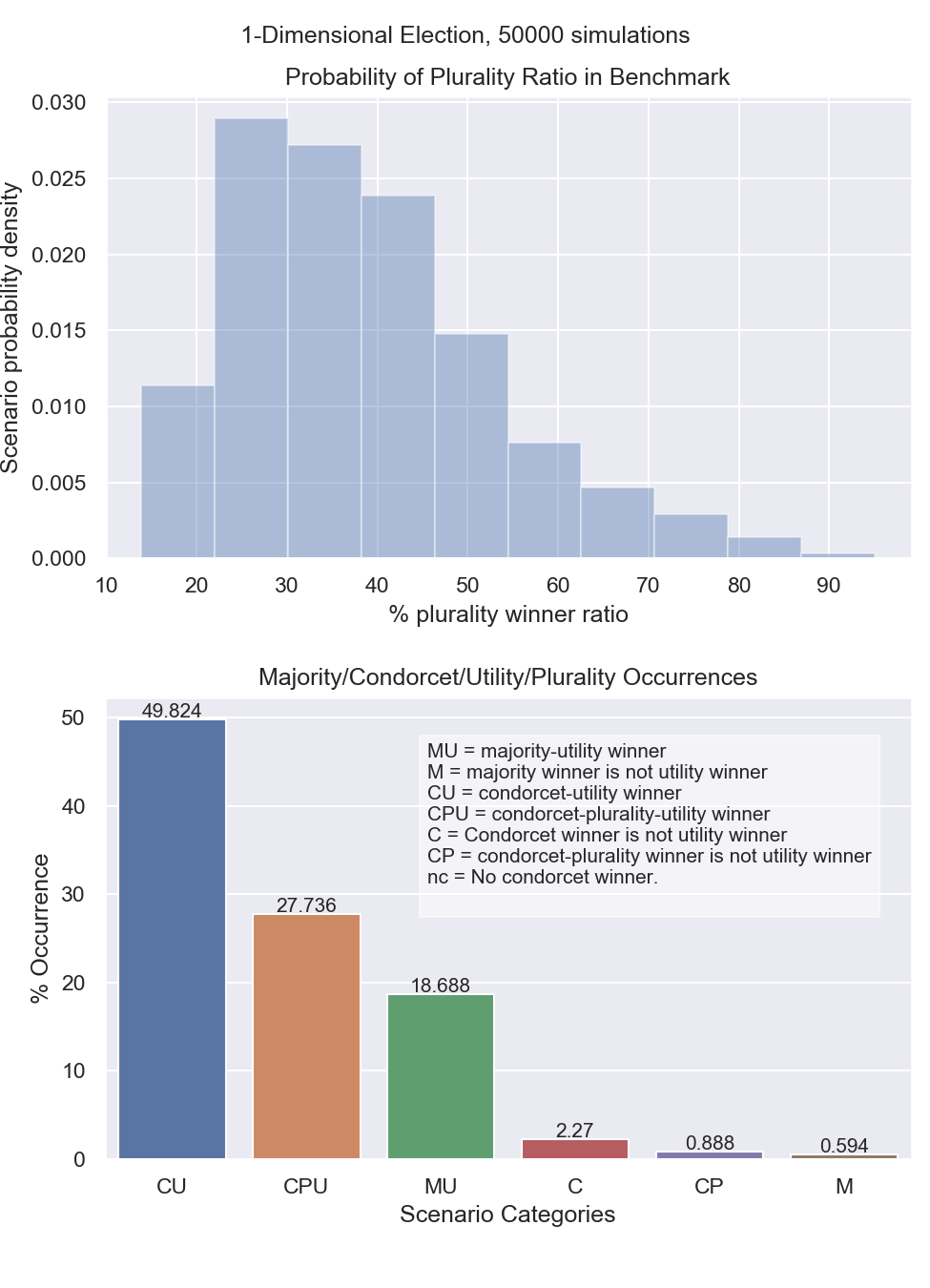
Figure 1: Scenario category probabilities for 1-Dimensional Spatial Model¶
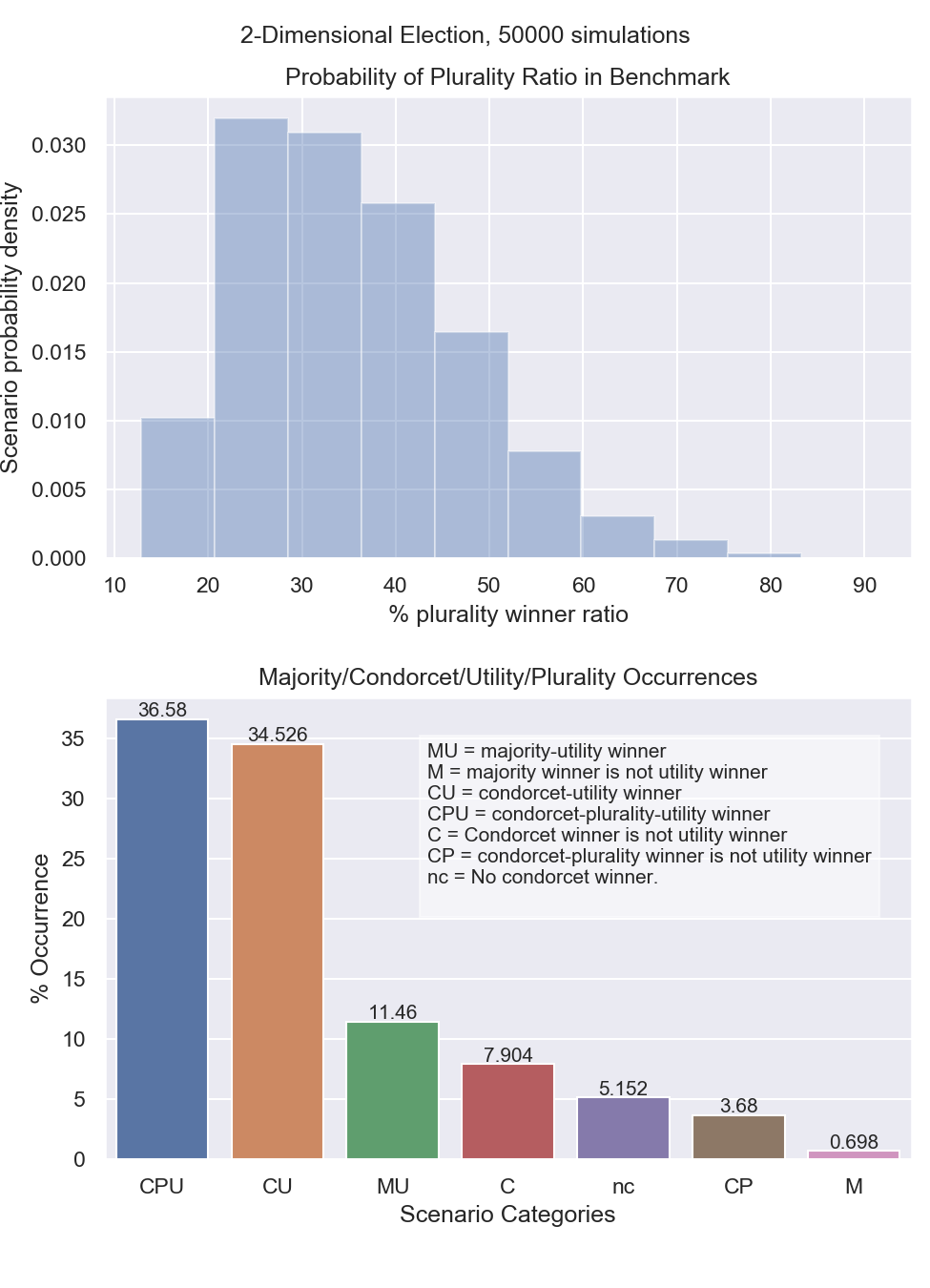
Figure 2: Scenario category probabilities for 2-Dimensional Spatial Model¶
Due to increasing Condorcet paradoxes and Condorcet failures, Cardinal and Hybrid voting systems have superior performance in multi-dimensional problems. Voter regrets, normalized as in the previous report, are plotted below in Figure 3 and 4 for 1 and 2 dimensional models.
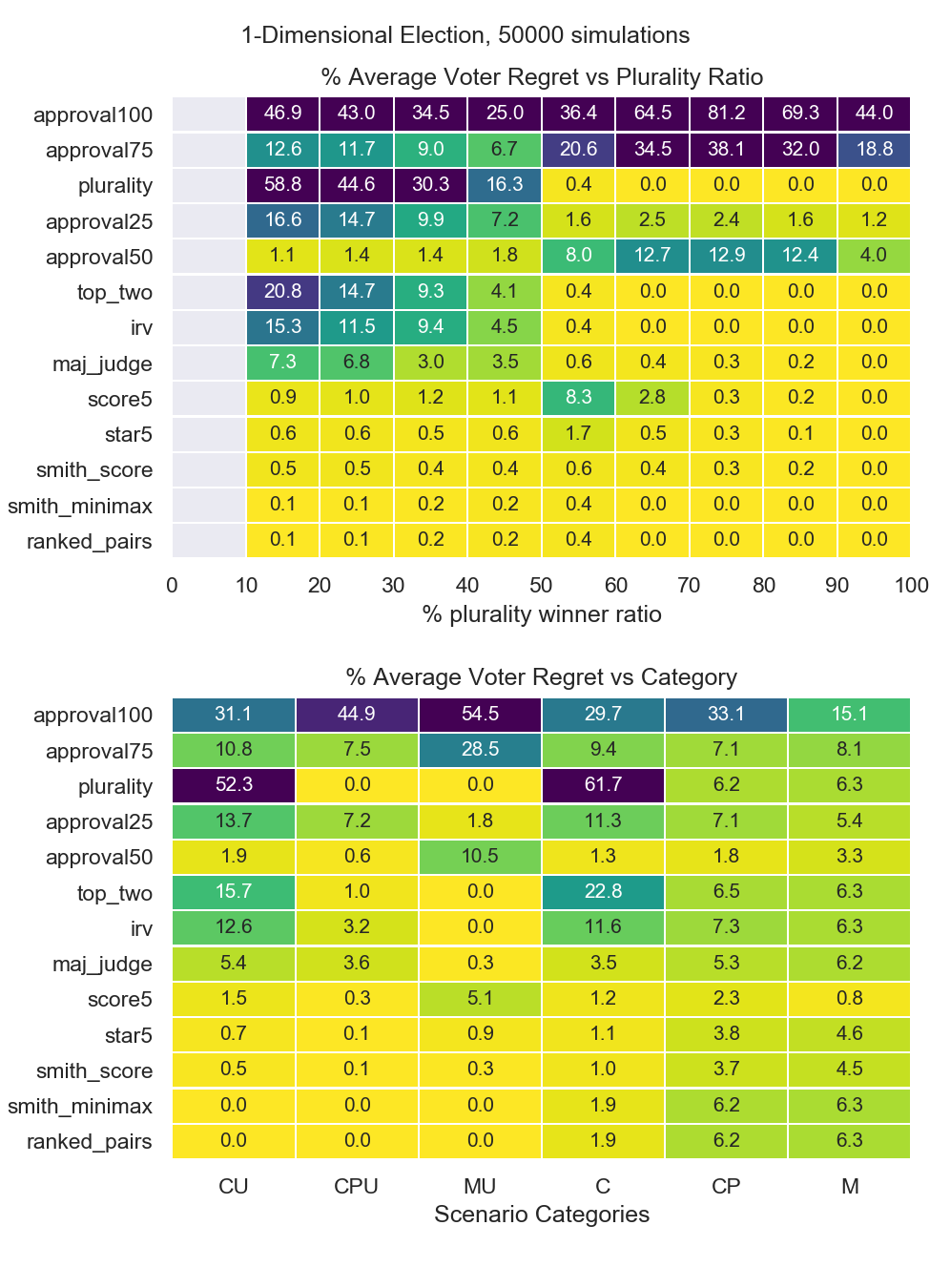
Figure 3: Voter regrets for 1-Dimensional Spatial Model¶
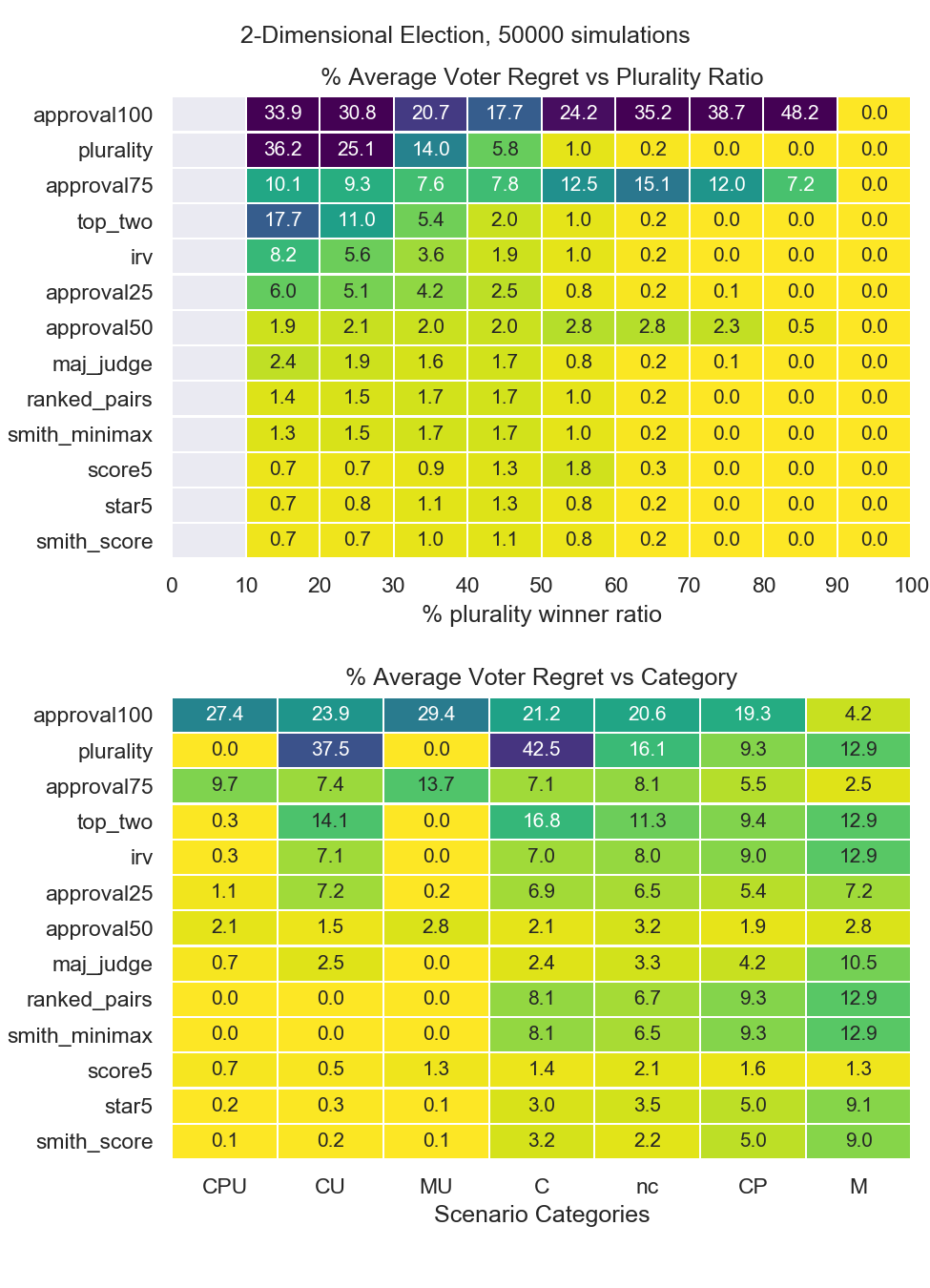
Figure 4: Voter regrets for 2-Dimensional Spatial Model¶
Increasing Preference Dimensionality to 3, 4, and 5¶
Further increasing preference dimensions to 3, 4, and 5 dimensions increases the prevalence of the easiest-to-solve scenario category “CPU”, where the Condorcet, plurality, and utility winner are coincident. All other more complex scenario prevalences are reduced with each additional dimension.
Therefore for a “conservative” (in terms of engineering risk aversion) assessment of a voter method, it ought to be sufficient to only assess the 1-dimensional and 2-dimensional cases which contain the greatest occurrences of voting system failure scenarios.
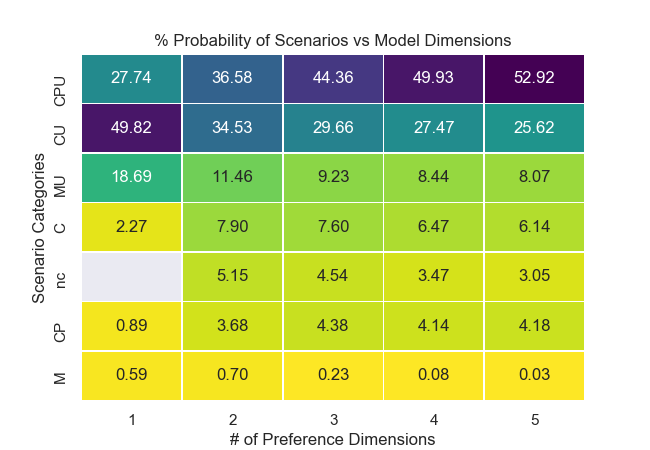
Figure 5: Occurrences of Scenarios vs Model Preference Dimensions¶

Figure 4: Voter regrets for 3-Dimensional Spatial Model¶
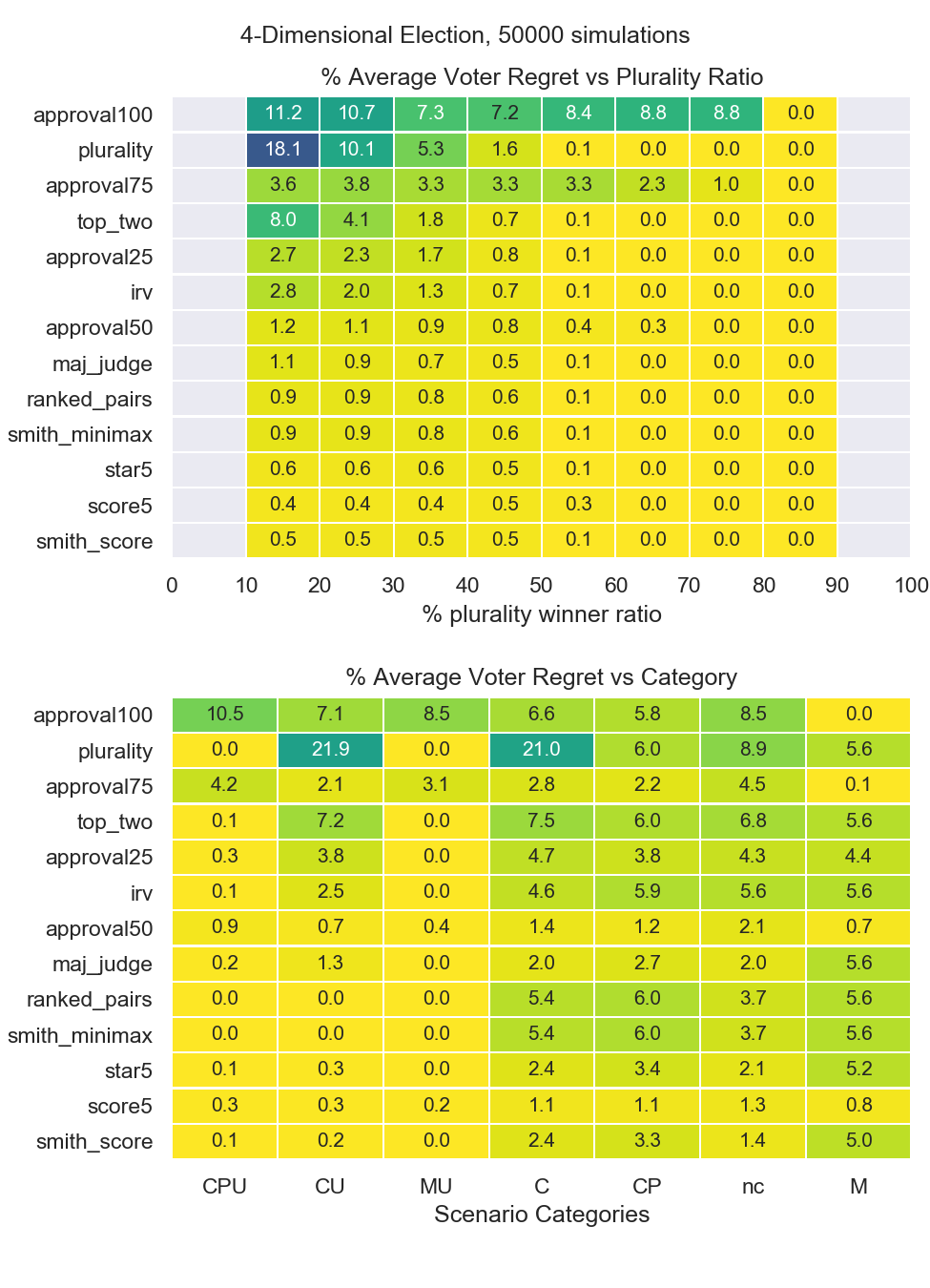
Figure 4: Voter regrets for 4-Dimensional Spatial Model¶
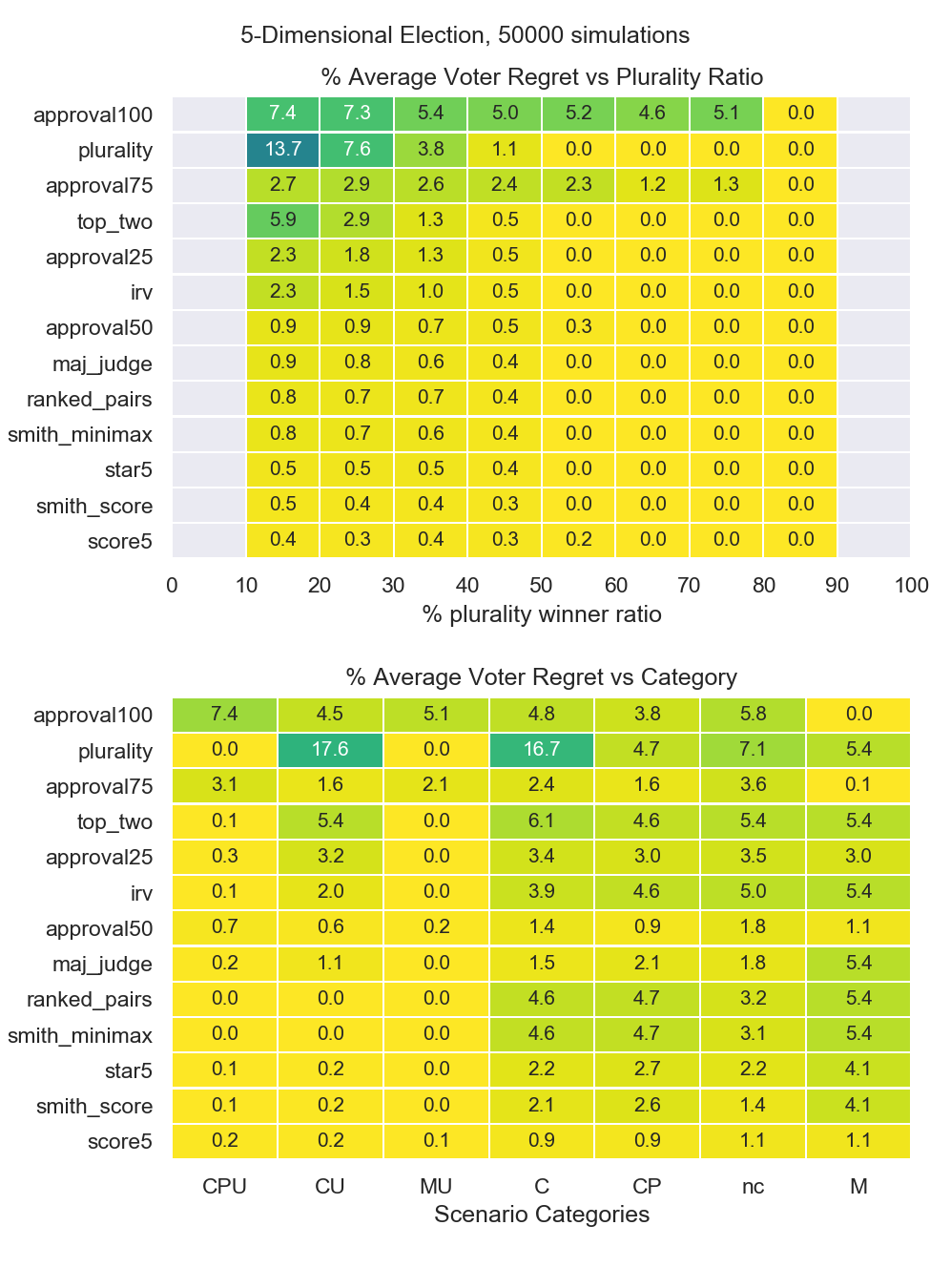
Figure 4: Voter regrets for 5-Dimensional Spatial Model¶
The Effect of Greater Number of Candidates¶
As the number of candidates increases, the likelihood of Condorcet failures tend to increase. For 2-dimensional models, the likelihood that the Condorcet winner is not the utility winner increases from 8.47% to 10.93% from 3 to 9 candidates. The likelihood of a Condorcet Paradox increases from 1.09% to 5.37%.
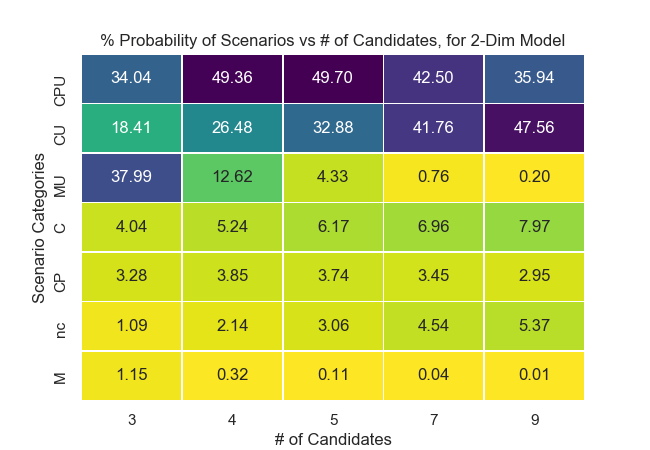
Figure 6: Occurrences of Scenarios vs # of Candidates¶
Conclusions¶
STAR voting or a similar hybrid cardinal method is recommended for multi-dimensional problems with higher occurrences of Condorcet Cycles. Condorcet methods remain well suited for 1-dimensionally polarized elections. Score also has excellent performance, assuming no tactical voting. Under min-max strategy equivalent to approval25 or approval50 voting, regret may be significantly increased.