Score Voting Utility Failure Case Study¶
John Huang, 18 May 2020
This report documents an observed score voting failure in electing the utilitarian winner.
A scored election case from the benchmark in Simple 3-Way Election Simulations for Alternative Voting Methods is examined in detail to determine the cause of failure.
The Case Study¶
An election case with the maximum regret found in all iterations was chosen for further analysis. The voter preference distribution and the candidate locations are plotted.
Our “Votesim” simulator assumes a linear mapping of preference distance to voter rating of a candidate. However, Votesim also normalizes scores so that the worst candidate for a voter is always given 0 score, and the best candidate for that voter receives full score. Voter scores for each candidate are generated with these assumptions in the 2nd subplot.
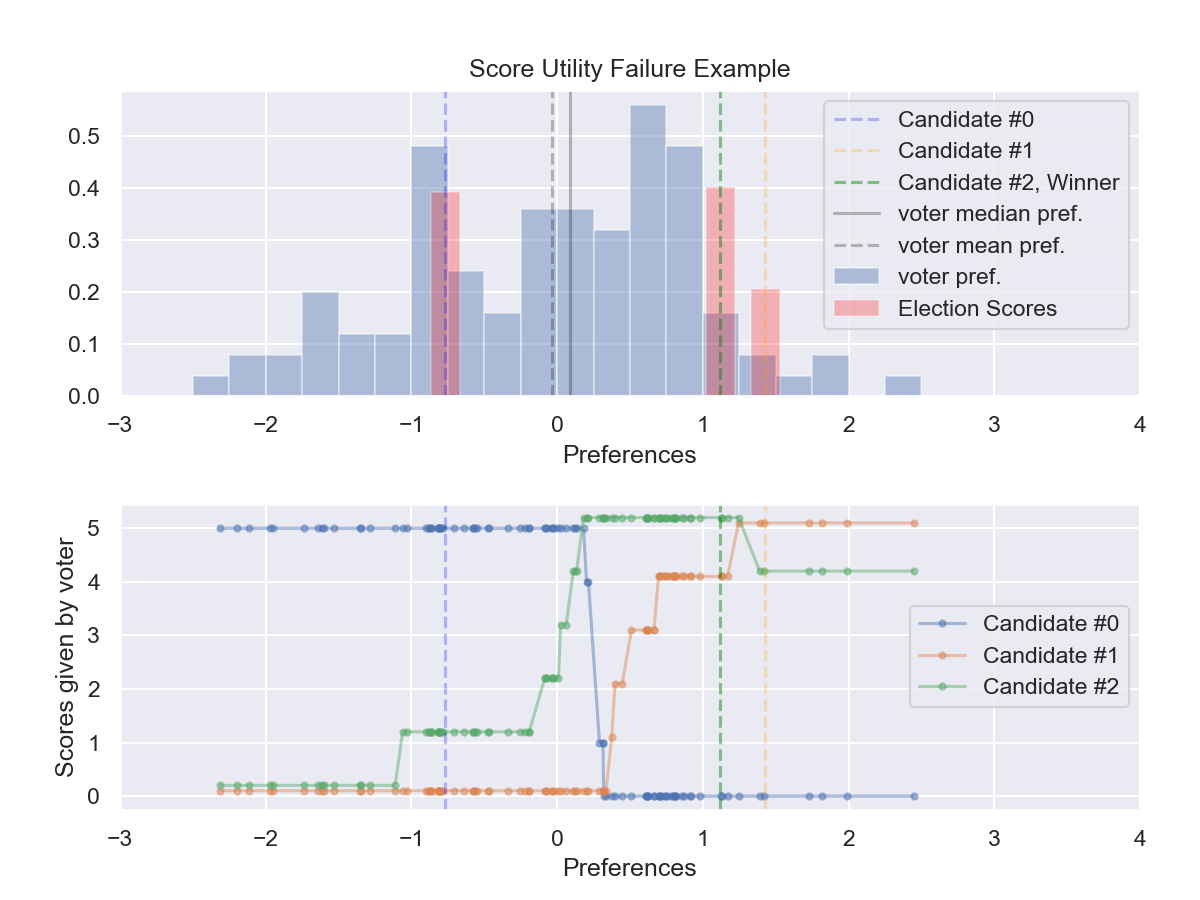
Figure 2: Candidate and voter preferences, and voter scores for candidates¶
In this election, 3 candidates were on the ballot, labeled #0, #1, and #2.
Candidate #0 is the utilitarian winner as the candidate closest to the mean and median preference point of the voters.
Candidate #1 is an extreme candidate, farthest from the preference centroid.
Candidate #2 is the median of the candidate population and is not the utilitarian winner.
- The coordinates of the candidates are:
Candidate #0 = -0.77
Candidate #1 = 1.43
Candidate #2 = 1.12
Voter Population Centroid = -0.03
- The average regrets (preference distance) for each candidate if they are elected are:
Candidate #0 = 1.02
Candidate #1 = 1.51
Candidate #2 = 1.24
- The total scores of the election are
Candidate #0 = 281
Candidate #1 = 148
Candidate #2 = 288 (Winner at approximately 0.98% score margin)
Observations¶
Although scored voting advocates claim that scored voting satisfies the independence of irrelevant alternatives (IIA) criterion, IIA is not satisfied in our election & voter behavior model.
Due to normalization, voters in this model do not vote proportionate to their utility. Take for example the voter scores vs preferences for Candidate #0. For voters far away from Candidate #0 on the left side at preference of -2, they award Candidate #0 full score (5’s) as for them, no other candidate is better. Voters with preferences equal to Candidate #0 also give #0 the same score, despite receiving far greater utility from #0. Normalization distorts true average utility.
In our behavior model, voters near Candidate #0 at preference = -0.77 have decided to “honestly hedge their bets” by giving Candidate #2 a score of 1 of 5. Voters decide to do this because of the existence of Candidate #1 whom they prefer even less, whom they give a score 0 of 5.
If candidate #1 did not exist, there would be no reason to give candidate #2 nonzero score. Candidate #1’s existence causes #0 to lose the election.
Comparison to Other Methods¶
In our example, Candidate #0 is the utility winner, the Condorcet winner, and the majority winner. Our scenario is correctly resolved by Condorcet methods, STAR voting (the runoff round corrects effects from normalization), and even plurality.
With STAR voting, #0 wins with a 7% margin of victory after the runoff
With Condorcet methods, #0 wins with a 6% margin of victory for Candidate #0 vs #2
With plurality, #0 wins with a 12% margin of victory.
Conclusions¶
The election observed in this report is a typical failure scenario for scored voting. As voters are more likely to give median candidates nonzero scores, scored voting has a bias in favor of the median of the candidate population.
Scores given by voters are not a true map to “utility”. Rational, self-interested voters would normalize their ballots, so that their most preferred candidate receives a full score, in order to maximize their electoral impact.
Voters are required to make very tough, strategic decisions on whether they ought to hedge and give non-favorite candidates a positive score. In our example election, the honest hedge for #0 supporters does not pay off but results in a loss.
Scored voting does not satisfy independence of irrelevant alternatives. Our scenario demanded that supporters of Candidate #0 recognize the strategic inviability of Candidate #1 and therefore rate both Candidates #1 and #2 0 out of 5.